Lab 6: Performance Optimization (Memory Hierarchy)
Overview
This lab will focus on how computer memory systems store data, and how the implementation of memory systems (especially the cache(s)) affects program performance. At the end of the lab, you will measure the performance of your computer memory system under different application behavior patterns.
Pre-Lab
There is no pre-lab activity for this lab.
Lab
To begin this lab, start by obtaining the necessary boilerplate code. Enter the class repository:
unix> cd ~/bitbucket/2012_fall_ecpe170_boilerplate/
Pull the latest version of the repository, and update your local copy of it:
unix> hg pull
unix> hg update
Copy the files you want from the class repository to your private repository:
(In this case, it is three folders you want)
unix> cp -R ~/bitbucket/2012_fall_ecpe170_boilerplate/lab06/part2 ~/bitbucket/2012_fall_ecpe170/lab06
unix> cp -R ~/bitbucket/2012_fall_ecpe170_boilerplate/lab06/part4 ~/bitbucket/2012_fall_ecpe170/lab06
unix> cp -R ~/bitbucket/2012_fall_ecpe170_boilerplate/lab06/postlab ~/bitbucket/2012_fall_ecpe170/lab06
Enter your private repository now, specifically the lab06 folder:
unix> cd ~/bitbucket/2012_fall_ecpe170/lab06
Add the new files to version control in your private repository:
(Technically, part2, part4, and postlab are directories, but Mercurial is smart enough to just add all the files in these directories with this command)
unix> hg add part2 part4 postlab
Commit the new files in your personal repository, so you can easily go back to the original starter code if necessary
unix> hg commit -m "Starting Lab 6 with boilerplate code"
Push the new commit to the bitbucket.org website
unix> hg push
Lab Part 1 - Data Storage in Memory
The C programming language, like most languages, supports multi-dimensional arrays. For example, your array could be declared as:
uint32_t array[10][20]; // An 2-dimensional array of 4-byte (32-bit) unsigned integers, i.e. uint32_t
While the array may be multi-dimensional, computer memory is not! Behind the scenes, the compiler is converting each array access into an equivalent access in a 1-dimensional array. How exactly is this done?
We can imagine several obvious possibilities:
- Option 1: Start at row=0, column=0. Step through each row until the end, then advance to the next column.
- Option 2: Start at row=0, column=0. Step through each column until the end, then advance to the next row.
- Other options? (Start at the last row/column, and store in reverse order?)
| Memory Address | Option 1 | Option 2 | ... |
|---|---|---|---|
| Memory[0] | array[0][0] | array[0][0] | |
| Memory[1] | array[1][0] | array[0][1] | |
| Memory[2] | array[2][0] | array[0][2] | |
| ... | ... | ... |
Assignment: Write a C program that demonstrates how two-dimensional arrays and three-dimensional arrays are actually stored in computer memory. Include a Makefile. The array can be static (i.e. you do not need to use malloc() as you did in the earlier C programming post-lab exercise).
There is no boilerplate code here. Just create a new part1 directory in the lab06 folder of your working repository, and get started!
unix> cd ~/bitbucket/2012_fall_ecpe170/lab06
unix> mkdir part1
unix> cd part1
Requirements:
- Use an example array like this in your program:
uint32_t array1[3][5]; // 2D array
uint32_t array2[3][5][7]; // 3D array - The output of your program must be understandable to a lay person! (i.e. not a trained computer scientist). Don't just print out some unlabeled memory addresses! The output of your program should clearly explain what is being done behind the scenes and how the results are to be read/interpreted.
- Your program must include a Makefile.
Lab Report:
(1) Describe how a two-dimensional array is stored in one-dimensional computer memory.
(2) Describe how a three-dimensional array is stored in one-dimensional computer memory.
(3) Copy and paste the output of your program into your lab report, and be sure that the source code and Makefile is included in your Mercurial repository.
Lab Part 2 - Memory Locality
Memory locality is **essential** in ensuring good application performance. There are two forms of locality to keep in mind when designing a computer system (either its hardware, or software!)
- Temporal locality: A memory address accessed once is likely to be accessed again in the near future.
- Spatial locality: If one memory address is accessed, other nearby memory addresses are also likely to be accessed.
The general rule is this: programs with good memory locality perform better than programs with poor memory locality. We'll learn some reasons why good locality improves program performance later in this lab.
Consider the following function that processes an array:
int sumarray(int a[ROWS])
{
int i, sum=0;
for (i=0; i<ROWS; i++)
sum += a[i];
return sum;
}
Does this function have good locality? This is not a question with a simple yes or no answer. It requires examining each variable in turn.
- Scalar variable i and sum: These variables are accessed on each pass through the loop, so they each have temporal locality. But, being a scalar, there is no guarantee of spatial locality. (i.e. There might be other data elements nearby that benefit, but we don't know for sure).
- Array variable a: Using our knowledge from Lab Part 1, we know how the array "a" is actually stored in computer memory. By tracing through the function, a table can be created that relates the memory address with the element of the array actually stored in that memory address, and the sequence (1, 2, 3, ...) that the array element is accessed when the function is run. For example, Table 1 below shows the access pattern for the sumarray() function.
Table 1: Access Pattern for sumarray() Assuming ROWS=8
| Memory Address | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
| Memory Contents | a[0] | a[1] | a[2] | a[3] | a[4] | a[5] | a[6] | a[7] |
| Program Access Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Note 1: Address assumes array starts at memory address 0.
Note 2: Table is sorted by ascending memory addresses, not by program access order.
Thus, from the table, the array exhibits good spatial locality (because elements are read sequentially), but poor temporal locality, because elements are only read once.
Below are three more functions: sumarrayrows(), summarraycols(), and sumarray3d().
int sumarrayrows(int a[ROWS][COLS])
{
int i, j, sum = 0;for (i = 0; i < ROWS; i++)
for (j = 0; j < COLS; j++)
sum += a[i][j];
return sum;
}
int sumarraycols(int a[ROWS][COLS])
{
int i, j, sum = 0;for (j = 0; j < COLS; j++)
for (i = 0; i < ROWS; i++)
sum += a[i][j];
return sum;
}
int sumarray3d(int a[ROWS][COLS][DEPTH])
{
int i, j, k, sum = 0;for (i = 0; i < COLS; i++) {
for (j = 0; j < DEPTH; j++) {
for (k = 0; k < ROWS; k++) {
sum += a[k][i][j];
}
}
}
return sum;
}
Lab Report:
(4) Provide an Access Pattern table for the sumarrayrows() function assuming ROWS=2 and COLS=3.
(5) Does sumarrayrows() have good temporal or spatial locality?
(6) Provide an Access Pattern table for the sumarraycols() function assuming ROWS=2 and COLS=3.
(7) Does sumarraycols() have good temporal or spatial locality?
(8) Provide an Access Pattern table for the sumarray3d() function assuming ROWS=2, COLS=3, and DEPTH=4.
(9) Does sumarray3d() have good temporal or spatial locality?
Lab Part 3 - Locality and Performance
In part 2, you observed how different algorithms have different temporal or spatial locality. Now let's relate locality to performance. Our goal is to deduce why locality has an impact on performance.
This section is based on in-class discussion.
Lab Report:
(10) Imagine that the memory system only had main memory (no cache was present). Is temporal or spatial locality important for performance here when repeatedly accessing an array with 8-byte elements? Why or why not?
(11) Imagine that the memory system had main memory and a 1-level cache, but each cache line size was only 8 bytes (64 bits) in size. Is temporal or spatial locality important for performance here when repeatedly accessing an array with 8-byte elements? Why or why not?
(12) Imagine that the memory system had main memory and a 1-level cache, and the cache line size was 64 bytes. Is temporal or spatial locality important for performance here when repeatedly accessing an array with 8-byte elements? Why or why not?
(13) Imagine your program accesses a 100,000 element array (of 8 byte elements) once from beginning to end with stride 1. The memory system has a 1-level cache with a line size of 64 bytes. No pre-fetching is implemented. How many cache misses would be expected in this system?
(14) Imagine your program accesses a 100,000 element array (of 8 byte elements) once from beginning to end with stride 1. The memory system has a 1-level cache with a line size of 64 bytes. A hardware prefetcher is implemented. In the best-possible case, how many cache misses would be expected in this system? Feel free to make assumptions like "the hardware prefetcher runs fast enough to stay ahead of the user program."
Lab Part 4 - Performance Measurement
For this part of the lab, you will compare the performance of two algorithms in an actual application for a variety of data sizes. The sample program measures the speed of the matrix computation C = C + A * B. The three matrices A, B, and C are all of size n*n, where n is passed to this program on the command line. The reported result is the number of double-precision (64-bit) floating point operations per second, which should be similar regardless of the specific numbers being multiplied and added. The matrices are initialized to a specific pseudo-random sequence for repeatability.
Two algorithms are used here. Algorithm 1 uses the conventional array access order. Algorithm 2 reverses the order in which the loops are accessed for better cache locality.
You should already have the boilerplate code for this part of the lab.
unix> cd ~/bitbucket/2012_fall_ecpe170/lab06
unix> cd part4
Compile the application:
unix> make
Run the application using algorithm 1 for a small 256x256 matrix:
unix> ./matrix_math 1 256
Assignment: Write a script (either for the Bash shell or in Python) that characterizes the application performance. Specifically, your script should automatically test both algorithms of the matrix math program for each of the array sizes shown in Table 2.
Extra Credit Option #1: Extend your script to automatically parse the output of the program, capture the number of FLOPS, and save it into a text file suitable for import into OpenOffice or other graphing program.
Value: +20 points on lab score
Extra Credit Option #2: Modify the provided program to count the non-sequential accesses in the matrix multiply algorithm. (Specifically, any time where the next element was more than 1 away from the previous element). Provide a table comparing algorithm 1 versus algorithm 2 on this metric for all of the array sizes tested previously.
Value: +25 points on lab score
Table 2: Array Sizes in Test Suite
| Algorithm 1 | Algorithm 2 |
|---|---|
| 256 | 256 |
| 512 | 512 |
| 768 | 768 |
| 1024 | 1024 |
| 1280 | 1280 |
| 1536 | 1536 |
| 1792 | 1792 |
| 2048 | 2048 |
Lab Report:
(15) Inspect the provided source code. Describe how the two-dimensional arrays are stored in memory, since the code only has one-dimensional array accesses like: a[element #].
(16) After running your experiment script, create a table that shows floating point operations per second for both algorithms at the array sizes listed in Table 2.
(17) After running your experiment script, create a graph that shows floating point operations per second for both algorithms at the array sizes listed in Table 2.
Note: No credit will be given for sloppy graphs that lack X and Y axis labels, a legend, and a title.
(18) Be sure that the script source code is included in your Mercurial repository.
Tips:
- To execute a script at the command line, it must be marked as "executable". If the name of your script (text file) is experiment.sh, you can mark it executable at the command line by running: chmod +x experiment.sh
- Example of a for-loop in a Bash script
- Example of a for-loop in a Python script
Post-Lab
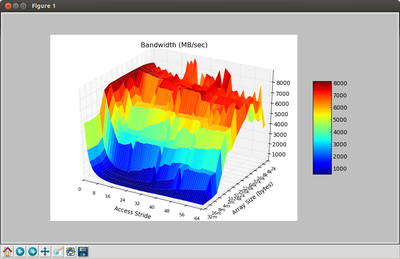
For this post-lab, you need to run the "Memory Mountain" program and display the results. For each experiment, this program creates an array of 8-byte values in memory (floating-point doubles). This array is then read from memory twice. The first time serves to "warm up" the cache (by reading in data from the array), while during the second time, the read bandwidth is measured. This bandwidth is simply the total number of bytes read from the array in a given second. A variety of experiments are conducted, in which the total array size and the read access pattern (called the stride) is varied. A stride of 1 indicates that every array element is read, a stride of 2 indicates that every other array element is read, etc...
To help us interpret the (eventual) results, obtain information on your CPU:
unix> cat /proc/cpuinfo
Post-Lab Report: Understanding your CPU
(1) Place the output of /proc/cpuinfo in your report. (I only need to see one processor core, not all the cores as reported)
(2) Based on the processor type reported, obtain the following specifications for your CPU from cpu-world.com or cpudb.stanford.edu
You might have to settle for a close processor from the same family. Make sure the frequency and L3 cache size match the results from /proc/cpuinfo!
(a) L1 instruction cache size
(b) L1 data cache size
(c) L2 cache size
(d) L3 cache size
(e) What URL did you obtain the above specifications from?
You should already have the boilerplate code for the postlab, including a "Memory Mountain" program and a Python script to plot the output.
unix> cd ~/bitbucket/2012_fall_ecpe170/lab06/postlab
Compile the memory mountain program:
unix> make
Run the memory mountain program, and save the output to a file called results.txt. Make sure your computer is as *IDLE* as possible while performing this test.
For perfect results, we would run this program on a bare computer without an operating system or other programs. Your current test environment, with a virtual machine (running an OS and other programs) inside a real OS (running the virtual machine manager and other programs) is definitely NOT IDEAL!
unix> sudo nice -n -20 ./mountain > results.txt
- The program is called "mountain"
- The nice utility allows us to set the priority of the program as high as possible. This requires root access (via sudo)
Run the Python / Matplotlib graphing script. Note that this requires you to install the python-matplotlib package as listed on the original Virtual Machine setup tutorial.
unix> ./plot.py results.txt &
Maximize the window to full screen for a better view.
Click-and-drag the graph to examine it from different angles.
Post-Lab Report: Understanding the Experiment
(3) Why is it important to run the test program on an idle computer system?
Explain what would happen if the computer was running several other active programs in the background at the same time, and how that would impact the test results.
(4) What is the size (in bytes) of a data element read from the array in the test?
(5) What is the range (min, max) of strides used in the test?
(6) What is the range (min, max) of array sizes used in the test?
Post-Lab Report: Interpreting the Results
(7) Take a screen capture of the displayed "memory mountain" (maximize the window so it's sufficiently large to read), and place the resulting image in your report
(8) What region (array size, stride) gets the most consistently high performance? (Ignoring spikes in the graph that are noisy results...) What is the read bandwidth reported? Annotate your figure by drawing an arrow on it.
(9) What region (array size, stride) gets the most consistently low performance? (Ignoring spikes in the graph that are noisy results...) What is the read bandwidth reported? Annotate your figure by drawing an arrow on it.
(10) Using LibreOffice calc, create two new bar graphs: One for stride=1, and the other for stride=64. Place them side-by-size in the report.
No credit will be given for sloppy graphs that lack X and Y axis labels and a title.
You can obtain the raw data from results.txt. Open it in gedit and turn off Text Wrapping in the preferences. (Otherwise, the columns will be a mess)
(11) When you look at the graph for stride=1, you (should) see relatively high performance compared to stride=64. This is true even for large array sizes that are much larger than the L3 cache size reported in /proc/cpuinfo.
How is this possible, when the array cannot possibly all fit into the cache? Your explanation should include a brief overview of hardware prefetching as it applies to caches.
(12) What is temporal locality? What is spatial locality?
(13) Adjusting the total array size impacts temporal locality - why? Will an increased array size increase or decrease temporal locality?
(14) Adjusting the read stride impacts spatial locality - why? Will an increased read stride increase or decrease spatial locality?
(15) As a software designer, describe at least 2 broad "guidelines" to ensure your programs run in the high-performing region of the graph instead of the low-performing region.
Post-Lab Report - Wrapup:
(1) What was the best aspect of this lab?
(2) What was the worst aspect of this lab?
(3) How would you suggest improving this lab in future semesters?
"Memory Mountain" program from "Computer Systems: A Programmer's Perspective", Second Edition, by Randal E. Bryant and David R. O'Hallaron